Vous souhaitez apprendre à coder en Python ? Ci-dessous, je me suis fais un petit aide-mémoire quand justement ma mémoire flanche un peu. Je ne sais pas si cela pourra aider quelqu'un d'autre que moi, mais si c'est le cas, alors je suis content de pouvoir le partager...
Numelion
Admin systèmes | Bureautique | Web
Bienvenue sur mon site. Je m’appelle Fabien et je suis le créateur du blog Numelion.com.
Je partage avec vous sur l’administration système, la bureautique et la création de projet web à travers des astuces, ressources ou tutoriels.
ADMINISTRATION RESEAUX & SYSTEMES
Dans cette partie du blog, vous trouverez des articles sur les systèmes d’exploitaiton pour les serveurs, comme Linux ou Windows Server.
Mais également des articles sur la création de script, par exemple pour Python ou Powershell. J’ai également créé des articles sur la gestion des bases de données comme MySQL.
Il s’agit d’articles que j’utilise pour me souvenir des différentes manipulations techniques.
BUREAUTIQUE / GESTION
C’est le premier type de contenu qui a été développé sur le blog. Les tutoriels sur les logiciels en bureautique. Vous trouverez des articles sur Excel, Word et bien d’autres outils pour améliorer votre productivité.
En plus de la bureautique, je réalise également des tutoriels plus spécifiques sur la gestion informatique. Par exemple, sur la mise en place de réseaux informatiques ou de logiciels liés à ces derniers.
PROJET WEB
Si vous souhaitez développer un projet sur internet, alors cette catégorie est pour vous. J’aborde la création de contenu, la gestion de site web et comment faire connaître votre travail.
En effet, le numérique a pris une place importante dans nos vies et cela va encore s’accélérer. Dès lors, créer son propre projet sur internet est une réelle opportunité. Je partage mes propres retours d’expérience.
Formation Gratuite Pour Créer Un Site Web / Blog
Un site internet occupe une place centrale dans une stratégie digitale. Lorsqu’on utilise des plateformes externes pour développer son activité, nous devons nous adapter. Avec un site internet, on peut centraliser des points stratégiques (pages de vente, pages de service, pages de capture d’email, produits, contenu texte…), les gérer et développer ce que l’on souhaite.
C’est un élément que l’on peut faire évoluer sans attendre et en fonction de ses besoins. On peut centraliser sur ce site tous les contenus clés que l’on souhaite présenter à son audience ou à ses clients selon le type d’objectif que l’on s’est fixé (créer une communauté, vendre des produits ou services, acquérir des contacts clients…).
Si vous souhaitez créer un site internet et que vous ne l’avez pas encore fait, je vous invite à découvrir ma formation gratuite et librement accessible pour vous lancer. Vous trouverez un processus étape par étape pour créer un site internet.
Elle dure près de 5 heures et vous permettra d’acquérir les connaissances de base pour créer un site internet ou un blog. Il suffit de cliquer sur le bouton à droite pour commencer.
Créer du contenu
Lorsque vous aurez créé un site internet / blog, il faudra alimenter ce dernier en contenu. Vous avez probablement déjà entendu cette phrase de Bill Gates, « le contenu est roi ». Sur Internet c’est la vérité, si vous ne créez pas de contenu, vous n’allez pas transformer votre site en réussite. La création de contenu (de qualité) est un pilier pour réussir.
Pour vous donner un exemple, plus vous allez créer de contenu, plus vous allez multiplier les opportunités d’être vu. Plus vous allez créer de contenu sur votre thématique, plus vous multipliez les chances d’apparaître dans les résultats des moteurs de recherche. Bien entendu, vous n’allez pas créer du contenu pour créer du contenu.
Il faudra créer un contenu optimisé pour le référencement naturel SEO. Une fois que ce contenu est créé, vous pouvez le partager à travers différents canaux d’acquisition de trafic. Ainsi, vous allez créer des ponts entre des visiteurs potentiels et votre site internet. L’objectif, faire venir les visiteurs sur ce dernier et créer une audience.
Si vous vendez des produits ou services, le contenu est l’une des premières étapes pour créer une relation de confiance. Pour transformer un visiteur en acheteur, il faut déterminer son parcours client. Une des premières étapes, c’est la recherche d’information. L’objectif, apparaître (le mieux placé) dans les réponses lorsque ce dernier lance ses recherches.
Faire connaître votre projet
Pour faire connaître son projet, il va falloir construire des ponts qui vont permettre d’attirer des visiteurs. Des ponts qui vont permettre de relier notre contenu et les visiteurs qui souhaiteraient découvrir ce contenu. Il faut viser les internautes intéressés par la thématique.
Pour cela, nous allons devoir varier les différentes sources d’acquisition de trafic. L’idéal est de cibler plusieurs sources et non une seule source. Choisir une seule source est risquée dans une stratégie de développement, si la source est coupée, vous n’avez plus de trafic.
Je pense qu’il faut miser sur plusieurs sources pour réussir ce développement. À l’inverse, il ne faut pas essayer d’être présent partout coûte que coûte (si vous n’avez pas le temps de tout gérer). Si vous êtes présents partout sans la possibilité de gérer cette présence, vous risquez de n’être présent nulle part. Il vaut mieux cibler les sources d’acquisition que vous souhaitez développer en priorité et dans la durée plutôt que de vouloir être partout.
Désormais, il faut choisir les sources et les développer pour alimenter le site internet en visiteurs.
Rentabiliser votre site internet
Enfin, abordons un point clé pour transformer un site en réussite. Les moyens de le rentabiliser. Premier point, quel type de site allez-vous créer ? Un ecommerce ? Un site vitrine ? Un blog ? Selon le type choisi, les moyens de générer des revenus seront différents.
L’objectif est de développer une relation de confiance qui sera durable avec son audience et ses potentiels futurs clients. Selon la solution que l’on va utiliser pour générer des revenus avec un site internet (e-commerce, site vitrine, blog infopreneur) on va adapter sa structure.
Une bonne solution est de créer une mixité entre les types de sites internet pour rentabiliser ce dernier. Un exemple, imaginons que vous ayez un site e-commerce. Sur ce dernier, vous pouvez créer des fiches produits pour les mettre en vente. Mais vous pouvez aussi mettre en place des pages de services (consultant, coaching…). Enfin, ajouter un blog qui aura pour objectif la génération de contenu pour attirer du trafic que vous souhaiterez ensuite transférer sur vos pages stratégiques (page produits, vente, formulaire de contact…).
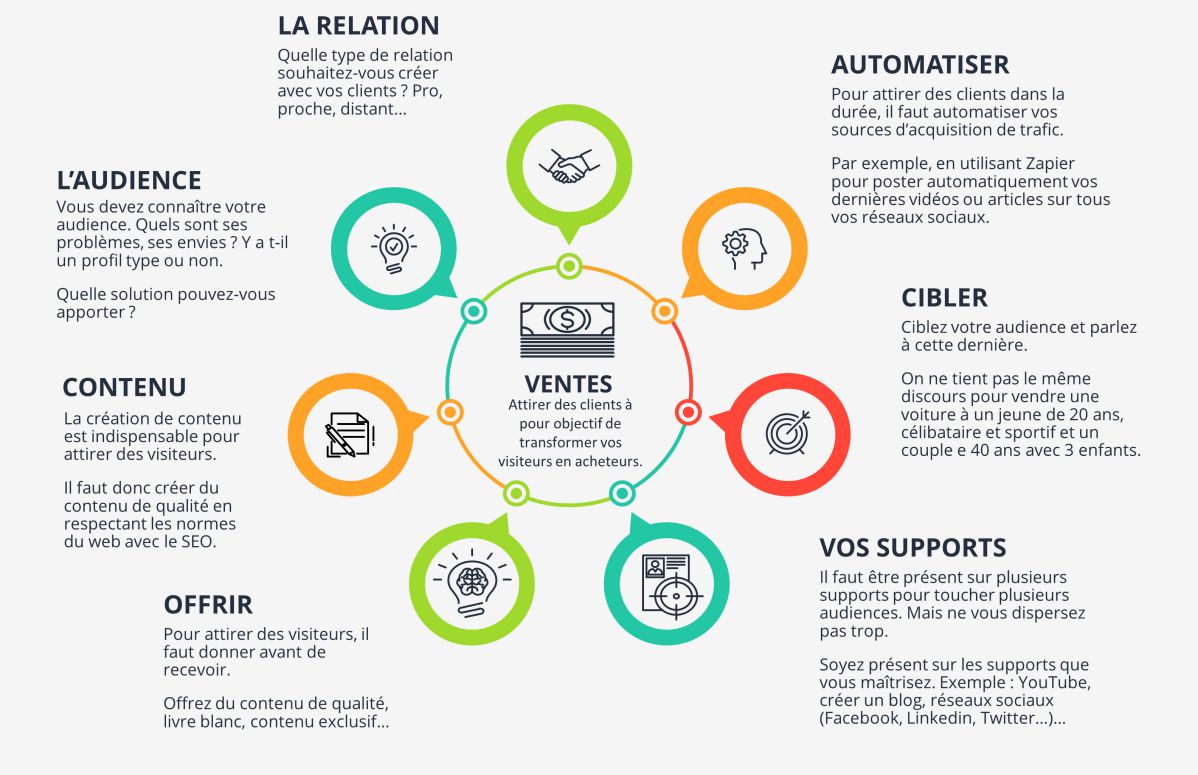
On en revient à la place centrale et stratégique d’un site internet dans le développement de son projet numérique. Cliquez sur l’image à gauche pour découvrir un exemple d’infographie complète qui concerne la rentabilisation d’un site pour les infopreneurs.
Des guides qui peuvent vous intéresser
INSTALLER ACTIVE DIRECTORY
Active Directory est l’un des principaux services déployés sur un serveur Windows Server.
Dans ce guide, nous verrons les différents points à mettre en place pour installer AD, mais aussi comment mettre en place le contrôleur de domaine pour pouvoir ensuite gérer nos différents utilisateurs sur le réseau.
CONFIGURER LE ROUTAGE CISCO
Cisco est une entreprise qui est bien implanter pour la création et la gestion de réseau informatique. Son matériel est très utilisé avec son OS.
J’ai réalisé plusieurs tutoriels sur le paramétrage des outils Cisco, un que je vous propose de découvrir est la configuration du routage Inter-Vlan.
Créer base de données Access
Vous connaissez probablement Word ou Excel dans la suite Office, pourtant un autre logiciel est particulièrement intéressant c’est Access.
C’est un logiciel qui permet de créer et gérer une ou plusieurs base de données et donc d’organiser ses informations. Je vous propose plusieurs cours complets pour découvrir comment utiliser Access.
Rédaction en HTML
Pour créer du contenu HTML vous pouvez utiliser les éditeurs de texte tout prêt ou vous pouvez utiliser vous-mêmes les balises.
Personnellement, je préfère utiliser les balises pour faire exactement ce que je souhaite avec la mise en forme du texte. Ce guide vous présente toutes les balises à connaître pour mettre en forme votre contenu texte en HTML.
Référencer un site / blog
Le référencement naturel SEO est un ensemble de bonnes pratiques. Dans ce guide, je vous propose de faire un tour des principaux points sur lesquels il faut être vigilant pour référencer un site internet.
Il faut appliquer ces règles pour l’ensemble du contenu (et la structure) que vous allez générer afin d’obtenir des résultats qui évolueront à la hausse dans le temps.
Créer un serveur web LAMP
Linux est l’un des systèmes d’exploitation les plus utilisés pour le déploiement de service et notamment de serveurs web.
On va généralement utiliser un ensemble de paquets. Je vous propose d’installer LAMP qui permet de déployer un serveur web rapidement avec Apache2.
Mes méthodes (un peu étranges certes)
Le contenu travail pour vous
Votre contenu est un employé commercial
Vous pensez qu’il faut créer du contenu pour créer du contenu ? Il faut voir le contenu comme un commercial. Chaque contenu que vous allez créer est un employé qui va travailler pour vous 24 / 24 et 7 jours sur 7.
Si vous commencez à penser comme cela, vous allez donner à chaque contenu / employé un objectif.
Par exemple, positionner un appel à l’action pour inciter vos visiteurs à agir. S’ils le font, votre contenu / commercial aura vendu. Bien entendu, comme pour tous les commerciaux, certains seront meilleurs que d’autres.
Méthodes des cercles
Vendez plus en entourant votre contenu
La génération de contenu est parfaite pour attirer du trafic. C’est vrai. Mais c’est surtout parfait pour attirer du trafic et convertir vos objectifs : vendre / faire remplir des formulaires de contact…
En procédant de manière méticuleuse, en encerclant vos produits de contenu, vous allez pouvoir faire découvrir ces derniers à vos visiteurs. Des produits ou des pages clés de votre site.
Votre contenu sera votre meilleur atout dans ce cas. Ici, toute la question réside dans l’encerclement de vos produits par du contenu qui aura pour mission de rediriger vers des pages stratégiques ou de vente.
Méthode de la pieuvre
Devenez le leader de votre thématique
Vous vous demandez comment devenir le leader de votre thématique ? Je partage avec vous quelques conseils pour atteindre cet objectif au travers du contenu.
La méthode de la pieuvre peut sembler simple lorsqu’elle est expliquée, mais attention, simple ne veut pas dire facile.
Elle demande généralement du temps ou de l’investissement financier (pour gagner du temps) afin de générer le contenu nécessaire pour atteindre les premières places. Il faudra la compléter avec les bonnes pratiques du référencement.
Qu’allez-vous trouver sur Numelion.com ?
Administration de site web
Gérer un site demande des compétences techniques. Il est intéressant de gérer la partie non visible d’un site internet.
Blogging
Le blogging permet de générer du contenu au format texte. On peut le mixer avec d’autres types de sites (e-commerce, vitrine).
Content Marketing
Le contenu est ce qui permet de se faire connaître. Déterminer une stratégie est essentiel pour savoir où l’on va.
E-commerce
Le commerce en ligne est l’un des secteurs d’activités les plus porteurs. On peut vendre ses produits dans le monde entier.
Inbound Marketing
L’Inbound Marketing définit les moyens de faire venir à soi des visiteurs plutôt que d’aller les chercher en leur courant après.
Infopreneur
C’est une forme d’entrepreneuriat sur le web qui permet de partager ses connaissances en vendant des produits d’information.
Référencement SEO
Le référencement naturel permet d’attirer du trafic qualifié sur son site. Le plus difficile est de le mettre en place.
Réseaux sociaux
Les réseaux sociaux sont un excellent moyen de se faire connaître sans dépenser une fortune dans la publicité.
WordPress
L’outil le plus utilisé pour créer un site / blog. Près d’un site sur trois est créé avec WordPress. Numelion est un exemple.
Derniers articles du blog
NETPLAN : Configurer une Interface Réseau Linux
Vous souhaitez configurer la carte réseau de votre machine Linux avec Netplan ? Alors cet article devrait vous aider. Nous verrons comment procéder étape par étape, mais vous verrez que c'est relativement rapide. Lorsqu'on commence à paramétrer un serveur Linux, la...
Installer Windows 11 dans une Machine Virtuelle Virtualbox
Comment installer Windows 11 avec VirtualBox ? je vous propose un article pas à pas pour installer votre machine virtuelle avec le système d'exploitation de Windows. Si vous essaye de l'installer comme Windows 10, vous aurez une erreur et vous ne pourrez pas continuer...
L’auteur
Je m’appelle Fabien et je suis le créateur du site Numelion. Sur ce dernier, je partage des conseils qui proviennent de mes retours d’expérience. Cela fait près de 10 ans que j’ai créé mes premiers sites internet / blog.
 J’ai pris la pleine mesure de la force d’un site internet dans une stratégie digitale dans une précédente entreprise. Après avoir mis en place un simple site (avec formulaire de capture) et un blog pour attirer des visiteurs, nous avons commencé à avoir des clients qui venaient vers nous, nous ne les démarchions plus (Inbound Marketing).
J’ai pris la pleine mesure de la force d’un site internet dans une stratégie digitale dans une précédente entreprise. Après avoir mis en place un simple site (avec formulaire de capture) et un blog pour attirer des visiteurs, nous avons commencé à avoir des clients qui venaient vers nous, nous ne les démarchions plus (Inbound Marketing).
Depuis, je me suis lancé dans plusieurs projets digitaux et j’ai géré plusieurs sites internet / blog (tutoriels …).

J’ai ainsi pu acquérir ma propre expérience sur la création, la gestion et le développement d’un site web ainsi que son environnement (réseaux sociaux, système de vente…).
C’est celle-ci que je partage avec vous désormais. Pour en savoir plus, vous pouvez consulter la page à propos.